A  ENGENHARIA  DO  SOM

Copyright (c) A.C.Mattos

Um som é produzido quando há uma vibração em um ponto de um meio material (ar, água, ferro etc.). Quando batemos com um martelo em uma barra de ferro, a pancada produz uma rápida vibração no ponto de contacto, que se propaga pela barra e depois passa para o ar, espalhando-se através de superfícies esféricas, e diminuindo em intensidade até ser absorvido pelo meio.

Assim, o som nada mais é que uma variação rápida da pressão em um meio material. No vácuo, onde não há meio material, o som não se propaga.

A VELOCIDADE DO SOM

A velocidade do som depende apenas do meio em que se propaga, segundo a lei:

              (1)

onde

Compress = Módulo de compressibilidade adiabática volumétrica (cm²/kgf). Indica qual a diminuição relativa do volume do material  para um rápido aumento unitário da pressão. É o inverso do Módulo de Elasticidade Volumétrico ("Bulk Modulus of Elasticity").

Dens = densidade do material (g/cm³)

A velocidade de 1192 km/h também é chamada de Mach 1, ou "barreira do som" na aviação. Um deslocamento acima dessa velocidade se chama supersônico, caso dos aviões de caça e dos projéteis de arma de fogo. Na água, os submarinos usam o Sonar, um tipo de radar que funciona com pulsos sonoros de alta frequência (quanto maior a frequência, mais direcional é o som), que se propagam a 5167 km/h.

Conceitualmente, a velocidade do som depende apenas da variação da densidade do material com a pressão aplicada. Esta variação é igual ao produto da compressibilidade pela densidade. Como as densidades e as compressibilidades dos materiais são amplamente divulgadas e conhecidas, fica mais fácil usar a fórmula da velocidade com definida acima.

Se a temperatura variar, então, para o ar, a velocidade do som será dada por:

              (2)

baseado na equação dos gases perfeitos.

PRESSÃO ACÚSTICA E POTÊNCIA ACÚSTICA

Quando uma onda sonora se propaga em um meio, ela transporta uma potência acústica média (RMS) por unidade de área (perpendicular à direção da propagação) chamada de Intensidade Acústica, medida em watts por cm². É um processo semelhante às ondas que caminham por um lago tranquilo, quando atiramo-lhe uma pedra.

A propagação, em sua forma mais simples, se dá pela variação senoidal da pressão em um ponto do meio material. A pressão é medida em microbar (=dina/cm²=miligrama-força/cm²). Nessas condições, a Intensidade Acústica transmitida pelo som é:

                    (3)

Por exemplo, o som menos intenso que podemos ouvir tem uma pressão com amplitude de 0.0003 microbar (a pressão exercida por um peso de 0.3 microgramas em 1 cm²). A Intensidade Acústica correspondente é

O som mais intenso que o ouvido suporta tem uma pressão com amplitude de 280 microbar (a pressão exercida por um peso 280 miligramas/cm²) sendo sua Intensidade Acústica:

Assim, o ouvido humano consegue detectar sons em uma relação de 1 para 10¹² W / cm².

O SOM DIGITAL

Um som "puro" (ou Tom) é constituído por uma variação continua da pressão com uma frequência fixa. Por exemplo, a nota Lá (um som de referência para afinação de instrumentos), produz uma vibração de 440 ciclos por segundo (ou 440 Hertz = 440 Hz) no ar. Ela também pode ser "vista" na fig. 1 com o CoolEdit (um dos melhores softwares para a edição profissional de áudio). A parte de cima é o canal estéreo esquerdo, e a de baixo, o canal direito.

O eixo horizontal (X) mostra o tempo decorrido, enquanto a pressão do ar em um ponto aumenta e diminui. Como a frequência é de 440 Hz, o tempo de um ciclo é 2.27 milisegundos (ms), ou 1/440 (um ciclo da senóide demora um tempo dado pelo inverso de sua frequência).

 

O eixo vertical (Y) indica a amplitude da senóide. Na figura 1, a amplitude está indicada como percentagem do valor máximo que o arquivo MP3 (ou wave, .wav) aceita, que é 32768 (a metade de 2 elevado a 16 bits), para um som de 16 bits. Nessa escala, 1% = 327 em decimal. A senóide é constituída por pontos, pois o som digital é um conjunto de amostras (samples) do som original. Unindo-se os pontos (interpolação), obtém-se o som original. Essa união é feita pelo DSP (digital signal processor), o chip do CD player que lê o sinal digital, transforma-o em analógico, e o envia para o alto-falante via amplificador de som. Na gravação (via placa de som, por exemplo), o DSP recebe o sinal analógico e o amostra 44.100 vezes por segundo, gerando o sinal digital da fig.1.

 

Quanto maior o número de pontos, mais fielmente a interpolação representará o som original. O padrão é 44100 Hz (ou 44100 amostragens por segundo). Este valor deve ser maior ou igual ao dobro da máxima frequência do som original, esta estabelecida em 22.05 kHz (o ouvido geralmente detecta até 16 kHz). A fidelidade ao som original também depende do número de dígitos usados para representar a amplitude. O padrão estabelecido foi 16 bits (que usa pouco mais de 4 dígitos decimais: 0 a 32768). O padrão para CD é 44.1 kHz, 16 bits, para cada canal estéreo.

 

 

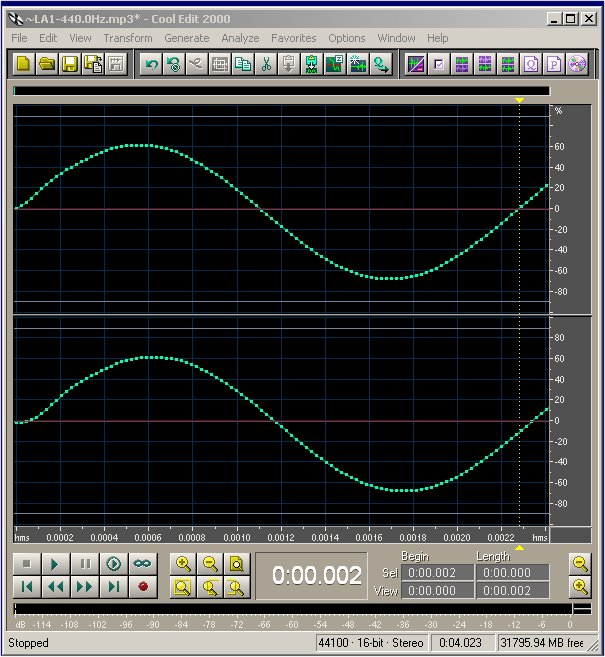
Figura 1: a nota Lá, de 440 Hz, vista no Cool Edit a partir de um MP3

 

SONS COMPLEXOS

 

O movimento oscilatório do ar produzido por um som raramente é uma senóide com frequência fixa, mas sim uma soma de senóides com frequências e amplitudes diferentes, e com deslocamentos uma das outras (Fase da senóide). Felizmente, um matemático francês, Jean Baptiste Joseph Fourier (1768-1830), demonstrou que qualquer forma de onda é a soma de muitas senóides de diferentes características. Por exemplo, cada instrumento tem um som típico, chamado de Timbre, e pode ser decomposto numa soma de senóides. Essa decomposição se chama Espectro do Som, e é feita por programas chamados FFT (Fast Fourier Transforms). O CoolEdit mostra o espectro de qualquer som.

 

 

 

     Fig.2  Fourier

 

O DECIBEL

 

Lidar com grandezas muito pequenas, como o limiar da audição (10^-16 W/cm²), ou com grandes variações, como a faixa de Intensidades audiveis (10¹² W/cm²) não é muito conveniente nos cálculos. Criou-se então uma outra forma de indicar os valores envolvidos em Acústica, trabalhando-se com as variações relativas das grandezas, e com os expoentes envolvidos. Assim, se uma grandeza é 10³ vezes maior que um valor de referência, então nos referimos a ela como 3 x 10 (o expoente vezes 10). Se for 10^-6 vezes menor, dizemos ser (- 6 x 10) (o expoente vezes 10). Em Acústica, quando se usam os expoentes dos valores relativos, eles são indicados com o sufixo decibel (dB), definido como:

 

                        (4)

 

A Intensidade de Referência (IR) foi naturalmente escolhida como o limiar da audição (10^-16 W/cm²), o que faz que o valor de IR seja, por definição, 0 dB. A Intensidade máxima audivel, (10^-4 W/cm² ), que é 10¹² vezes maior que IR, vale 120 dB.

 

O sufixo PWL (Power Level, ou Nivel de Potência) serve para indicar que os decibéis foram calculados pela fórmula (4).

 

Outra nomenclatura usual para o decibel é o dB-SPL, para o caso da Pressão Acústica (SPL = Sound Pressure Level, ou Nivel da Pressão Sonora). Neste caso, substitui-se na expressão (4) o valor dado em (3), obtendo-se:

 

                    (5)

 

onde 0.0003 microbar é a pressão minima audivel, correspondente à IR.

 

As nomenclaturas PWL e SPL servem para indicar a fórmula usada para calcular o dB.

Para medir o nivel sonoro se utiliza um Sound Level Meter (SLM), como o da Radio Shack, Modelo 33-2055, uso geral (US$ 50). Mede pressões sonoras de 50 a 128 dB-SPL (0 dB -> 0.0002 microbar), na faixa de 32 Hz a 10 kHz, com mostrador digital. Com esse aparelho pode-se determinar a equalização de um ambiente (com um equalizador). Veja esta aula de laboratório baseada nesse SLM.

Usando a linguagem dos decibéis, podemos afirmar que:

 

·         Não ouvimos sons com Intensidades menores que 0 dB-PWL ou que 0 dB-SPL.

·         O ouvido não distingue variações de Intensidade menores que 1 dB-PWL.

·         Uma conversação normal tem Intensidades em torno de 60 dB-PWL ou 60 dB-SPL.

·         Uma Intensidade maior que 120 dB-PWL (como em uma explosão) danifica permanentemente o ouvido.

·         A máxima pressão acústica suportada pelo ouvido é 120 dB-SPL.

·         Para dobrar a potência acústica emitida pelos alto-falantes, devemos aumentar a Intensidade em 3 dB-PWL.

 

 

O LOUDNESS E O FON

Loudness é o volume do som como percebido subjetivamente pelas pessoas. A potência acústica pode aumentar 1.26 vezes (1 dB, ou 26%), mas para o ouvido o volume permanece o mesmo. Pode aumentar 10 vezes (10 dB, ou 900%), mas o ouvido acha que o volume apenas dobrou. Ou ainda, a Intensidade pode ser de 60 dB (nivel de uma conversação normal), mas a 20 Hz o ouvido não percebe nada (volume zero), pois é surdo para essa Intensidade nessa frequência.

A medição exata do Loudness, ou Volume do Som, em FONS, é o resultado de uma pesquisa feita em 1933 por Fletcher e Munson (dois cientistas da Bell Laboratories, EUA), como mostrado na fig. 3. Cada curva horizontal mostra a pressão acústica necessária (em dB-SPL) para se ouvir todas as frequências com o mesmo volume de som. Nessa fig. 3, cada curva horizontal tem o mesmo número de "fons", ou seja, o mesmo volume, embora as pressões variem. O "fon" coincide com dB-SPL somente em 1 kHz (Tab 2):

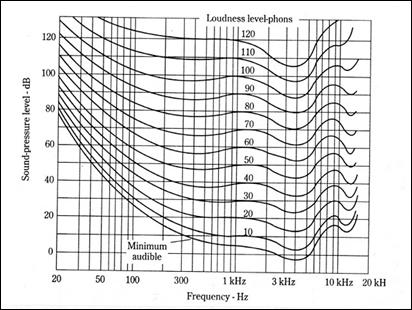
Figura 3: Curvas de Loudness de Fletcher e Munson (1933)
Cada curva indica a pressão acústica em dB-SPL para produzir
a sensação de volume igual em todas as frequências audíveis
Fonte: "Audio Cyclopedia", de H. Tremaine, fig. 1-76A

Assim, se ouvimos um som de 1 kHz com um volume de 10 fons (10 dB-SPL), então um som de 20 Hz deverá ser ouvido com uma pressão acústica de 80 dB-SPL, para que o volume se mantenha em 10 fons (isto é, para que ambos sons sejam igualmente escutados, sem predominância de um sobre o outro). Sem esse ajuste da pressão (equalização), os sons graves e agudos seriam ouvidos com um volume mais baixo que o de 1 kHz. Como exemplo, ouça estes sons de 100 Hz, 1 kHz e 10 kHz. Sem o botão Loudness ligado em seu equipamento de som, os sons grave e agudo vão ser ouvidos com volume menor que o médio (1 kHz), embora essas três senoides tenham a mesma amplitude (e produzam a mesma potência acústica com equalização plana).

Os amplificadores costumam ter um botão Loudness, que aumenta automaticamente o volume dos sons graves e agudos, segundo as curvas de Fletcher e Muson, permitindo ouvir todas as frequências com igual volume. Ou então possuem controles de graves, médios e agudos, com ajuste manual (este ajuste se chama equalização do som, e pode requerer um Medidor do Nivel Sonoro, SLM).

O SONE COMO ALTERNATIVA PARA O DECIBEL

As grandezas acústicas costumam ser indicadas em decibéis. Por exemplo, para dobrar o volume de um som de 1 kHz, aumenta-se a pressão acústica em 10 dB-SPL (fig. 3).

No entanto, ao invés de se falar "aumentar 10 dB", alguns podem preferir a frase "dobrar o volume".  O Sone é uma maneira de expressar uma grandeza em número de vezes o valor de referência, estabelecida em 40 dB-SPL (que é o nivel encontrado em uma biblioteca silenciosa, por exemplo).

Como a cada 10 dB o volume dobra (a 1 kHz), podemos construir uma escala em Sones, onde o volume de som a 40 dB seja igual a 1 Sone. Com 50 db teremos 2 Sones etc. A fórmula (6) permite construir essa escala:

       (6)

O AUDIOGRAMA

Para um som bem alto (80dB), as pessoas costumam ouvir frequências de 20 Hz a 20 kHz. Já para um som bem baixo (20dB), a faixa audivel vai de 200 Hz a 15 kHz.

A maior sensibilidade auditiva se dá na faixa de 1 kHz a 7 kHz. Somente 1% das pessoas ouve essas frequências abaixo de 0 dB. A maioria das pessoas (90%) só ouve essas frequências a partir de um volume de som de 20 sones.

O audiograma é o gráfico da sensibilidade auditiva de uma dada pessoa, determinado experimentalmente pelos fonoaudiólogos (ou na Internet). Ele mostra ser necessário maior volume de som para se ouvir os sons mais graves e os mais agudos (ou seja, o ouvido não tem uma "resposta plana" para todas as frequências). No entanto, ao contrários das curvas de Fletcher e Munson, que representam valores médios da população, o audiograma se refere a uma dada pessoa.

Na fig. 4, os pontos X indicam a sensibilidade do ouvido esquerdo, e os O indicam a do ouvido direito. A linha cinza continua mostra a sensibilidade minima "ideal" dos dois ouvidos.

Por exemplo, um som de 60 Hz (a frequência da rede de energia elétrica) precisa ter um volume de 40 dB para ser ouvido, enquanto que um outro de 1000 Hz pode ser escutado com um volume de 0 dB.

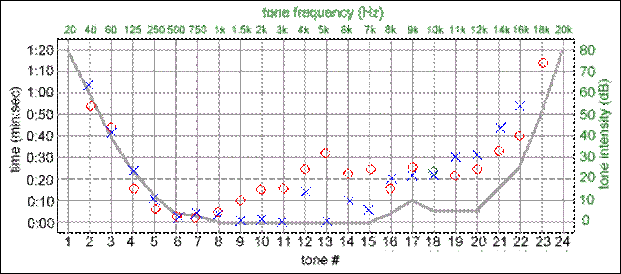
Figura 4: O audiograma de uma pessoa
http://www.digital-recordings.com/audiocd/audio.html

POTÊNCIA DE UM EQUIPAMENTO DE SOM

Uma Banda de Rock deseja que sua audiência, situada a 40 metros do palco, possa ouvi-la com um volume de som bem alto (90 dB-PWL). Para tanto, precisa saber a potência que seu equipamento de som deve ter. O conjunto de alto-falantes tem uma especificação do fabricante dada por 99 dB-PWL a 1.3 metros de distância, quando aplicado 1 W de potência em seus terminais elétricos. O conjunto comporta até 2.000 watts em seus terminais.

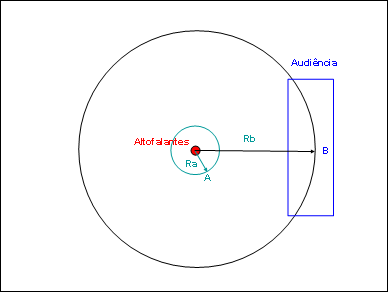
Figura 5: Medidas da área do Concerto de Rock

1. Pela especificação do fabricante:

Potencia acústica em um ponto A de uma esfera (fig. 5):

Pote * Potu * (4 * Pi * Ra² )            (watts)       [7]

onde

Pote = potência elétrica em watts que alimenta o alto-falante.

Potu = potência acústica unitária (em W/cm²), em um ponto A da esfera, em cujo centro estão os alto-falantes, quando alimentados com 1 Watt de potência elétrica.

Ra = Raio da esfera (dado pelo fabricante), onde Potu foi medido.

4 * Pi * Ra² = área da esfera por onde passa toda potência sonora gerada pelos alto-falantes.

2. No ponto B da esfera de raio Rb (com uma potência acústica Potb em W/cm²):

Potencia acústica em um ponto B da esfera:

Potb * (4 * Pi * Rb² )       (watts)               [8]

3. Apenas uma parte da potência que passa pela primeira esfera chega à segunda esfera, pois há perdas e atenuações no meio do caminho. Assim, dividimos a fórmula 7 por um número maior que 1, o coeficiente de perdas kperdas = Potp / Poto, e a igualamos à fórmula 8, obtendo:

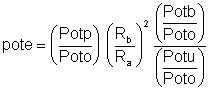                  (watts)         [9]

4. Como as especificações estão em decibéis, transformamos (9) para ser expressa em decibéis:

Da definição de decibel:

donde

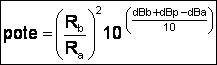               (watts)              [10]

onde

dBb = potência no ponto B, expressa em dB-PWL
dBp = potência perdida, expressa em dB-PWL
dBa = potência unitária em A, expresso em dB-PWL

5. Cálculo da potência do equipamento de som

Especificações do fabricante:

Ra = 1.3 metros
dBa = 99 dB

Especificação da Banda de Rock:

Rb = 40 metros
dBb = 90 dB

Perdas e atenuações:

dBp = 10 dB (geralmente)

Assim, deve ser enviada ao conjunto de alto-falantes uma potência de 1191 Watts RMS.

O equipamento de som, como um todo, deverá ter potência maior que 1191 W, pois também apresenta perdas elétricas.

OBS: A denominação RMS (Root Mean Square) ou "Potência Efetiva de Áudio", serve para diferenciar da "Potência de Pico" (PMPO ou "Potência Musical"), esta última usada pelo comércio, e sempre bem maior que a potência em RMS. Por exemplo, o equipamento de som "micro system MC-260" da Philips, anunciado no Estadão em 02-ago-2004 (p.I-9), tinha 20 watts RMS e 400 watts PMPO, ou seja, a potência efetiva (20 watts) era 5% da potência musical (400 watts).

A POTÊNCIA EM "RMS" E EM "PMPO"

O texto a seguir, que explica bem a diferença entre RMS e PMPO, foi obtido de http://www.fact-index.com/p/pm/pmpo.html e aqui traduzido.

PMPO significa "Peak Momentary Performance Output", ou "Saida de Pico do Desempenho Momentâneo". É uma medida duvidosa da potência de um alto-falante, mais de interesse para o comércio do que para os consumidores. O PMPO é calculado, pelo fabricante ou pelo testador de alto-falantes, como a potência máxima em watts, sob perfeitas condições, impossiveis de serem conseguidas com o uso normal do alto-falante. Nenhum sistema de som consegue manter sua potência PMPO por mais de uns poucos milésimos de segundo sem ser destruido.

Uma medida muito mais séria e confiável é o Watts-RMS. RMS significa "Root Mean Square", ou "Média Quadrática". O RMS é obtido tomando-se a média da potência máxima que o alto-falante aguenta, sem sofrer dano, por um longo periodo de tempo.

OBS. Matematicamente, a potência efetiva em Watts-RMS é obtida pela fórmula:

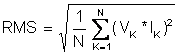
onde V_K e I_K são a tensão elétrica em Volts e a corrente elétrica em Ampères, fornecidas pelo equipamento de som, aos alto-falantes da caixa de som, em um instante K. O produto (V_K * I_K) é a potência elétrica instantânea, em watts, fornecida ao alto-falante no instante K. Existem aparelhos, os wattimetros, que medem automaticamente a energia consumida (semelhantes aos usados pela Eletropaulo e outras empresas para o cálculo da "Conta de Luz"). Observe que a potência efetiva não é igual ao produto da tensão efetiva pela corrente efetiva. Veja aqui mais detalhes.

Para se ter uma idéia da relação entre watts-PMPO e watts-RMS, considere os seguintes valores anunciados nos catálogos de alguns alto-falantes:

· TEAC PM-100 3D surround-sound speakers: 16 W-RMS, 180 W-PMPO

·         Kinyo 200W PC-speakers: 3 W-RMS, 200 W-PMPO

· Philips Fun Power Plus MMS-102 PC-speakers: 10 W-RMS, 120 W-PMPO (no entanto, a especificação da Philips menciona apenas o valor RMS; o valor PMPO é anunciado apenas pelos comerciantes)

Essa lista mostra que os valores da PMPO são muito exageradas, se comparados com os da RMS usados pelos profissionais.

A potência da corrente alternada, que inclui o áudio, é medida em watts-RMS, que é equivalente à potência usada no aquecimento em corrente continua. Este é um método honesto. Um dado amplificador com acoplamento direto (os transformadores são raros em equipamentos não usados nas redes elétricas de potência) pode obviamente variar sua saida de zero até no máximo VCC (máxima voltagem que alimenta o amplificador). Isto limita um simples amplificador de áudio de um carro a algo entre 12 V de variação, pico a pico na saida.

Por exemplo, um amplificador ideal (100% eficiente) com alimentação de 12 V (bateria do carro), pode comandar um sinal de amplitude 6 V. Em um alto-falante de 8 ohms, isto vai fornecer:

6V x 6V / 8 ohms = 4,5 watts de pico (máximo instantâneo)

Se o sinal for senoidal, seu valor RMS será 6V x 0,707 = 4,242 V-RMS. Esta voltagem, alimentando um alto-falante de 8 ohms fornece uma potência de:

4,242V x 4,242V / 8 = 2,25 watts-RMS

Com um alto-falante de 4 ohms, os valores dobram. Você pode notar qual valor o pessoal de marketing vai querer usar. Também pode observar por que alguns aparelhos de áudio do carro usam alto-falantes de 2 ohms.

Com uma saida diferencial (push-pull) do amplificador, a variação dobra, e a potência aumenta por um fator de 4. Assim, com uma alimentação de 14.4 VDC (VDC = voltagem constante), que é a máxima voltagem de uma bateria nova de carro, a máxima saida possivel para um alto-falante de 4 ohms é cerca de 14,4 x 14,4 x 0,707 / 4, ou em torno de 46 watts-RMS.

A "Potência Musical" (PMPO) é obtida usando-se um multiplicador meio arbitrário, baseado no fato de que amplificadores não podem fornecer potência máxima por muito tempo, mas podem fornecer alta potência durante curtos periodos (como na batida de um tambor). Isto faz com que possam reproduzir sons normais que tenham uma relação pico/média alta.

Para se obter mais potência, equipamentos avançados usam conversores DC-DC para gerar uma voltagem de alimentação mais alta que 12 V (às custas de maior consumo de corrente da bateria).

A potência verdadeira de saida de um amplificador pode ser estimada examinando-se a entrada DC. Amplificadores lineares tendem a ser em torno de 60% eficientes, no máximo. Um amplificador de carro, rotulado com "500W PMPO", mas ligado através de um fusivel de 5 ampères, pode fornecer uma potência máxima de 5A x 14,4V x 60%, ou cerca de 43 watts-RMS.

BIBLIOGRAFIA

Clássicos sobre Engenharia de Áudio

Harry F. Olson, "Music, Physics and Engineering" (McGraw-Hill, 1967)
Roger Darry, "PC Audio Editing" (Elsevier, 2003), para o CoolEdit
Lauro X. Nepomuceno, "Acústica Técnica" (Etegil Ltda., 1968)
Don & Carolin Davis, "Sound System Engineering" (Howard, 1978)
Leo Beranek (MIT), "Acoustics" (McGraw-Hill, 1954)
Leo Beranek (MIT), "Noise Reduction"  (McGraw-Hill, 1960)

Links

http://hyperphysics.phy-astr.gsu.edu/hbase/sound/soucon.html#soucon
http://www.acoustics.org/faqs.html
http://mathpages.com/home/kmath109/kmath109.htm
http://www.doh.ie/pdfdocs/hearing.pdf