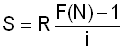
APÊNDICE 11
PERDAS MENSAIS
Sejam
R = remuneração média diária $ = salário mensal / 30 ou salário semanal / 7 etc. e
F (N) = (1 + i) N = fator de correção monetária
i = taxa diária de inflação
Tendo trabalhado no dia 1, o empregado deveria receber no fim do dia o valor R. Como só vai recebê-lo depois de N dias (N = 7 se pagamentos semanais, N = 30 se mensais etc.), deveremos corrigi-lo para o dia do pagamento. O valor de R corrigido será:
R . F (N - 1)
Para o dia 2, o valor corrigido será, analogamente,
R . F (N - 2)
e assim por diante.
Somando esses valores corrigidos, teremos o total devido (S) no dia do pagamento:
S = R . F(N - 1) + R . F(N - 2) + .... + R . F(1) + R
Como S é a soma de uma progressão geométrica de razão (1 + i ), primeiro termo R e total de N termos, seu valor será:
Esse seria o valor devido, em $. Entretanto, como o valor efetivamente recebido pelo empregado é (N.R), a perda mensal PM sofrida por causa da inflação terá sido de:
Substituindo S e efetuando vem, finalmente:
expresso como um fator do salário recebido.
Por outro lado, a taxa diária i é obtida a partir da taxa mensal imês, através da relação:
1 + imês = F (30)
Transformando a expressão de PM para incluir apenas a taxa mensal, vem:
Como exemplo de aplicação, temos:
Taxa mensal de inflação = imês = 10% a/m
Salário pago mensalmente: N = 30
T = (1 + 0,1)1/30 = 1,00318
A perda mensal PM será:
Por outro lado, se os pagamentos forem semanais, as perdas devidas à inflação diminuirão:
Sejam:
S = Salário inicial em $
N = número de meses decorridos entre dois reajustes salariais consecutivos
i = taxa mensal de inflação em 0/1
Após o primeiro mês, o salário corrigido vale S.F(1). Mas, como apenas foi recebido S, a diferença é a perda salarial após um mês: S.F(1) - S. Esta perda, sendo reposta na época do reajuste, deverá ser corrigida até essa data: [ S.F(1) - S ].F( N - 1 ) = S.F(N) - S.F(N-1).
Passado mais um mês, o mesmo raciocínio se repete, e a nova perda corrigida para a época do reajuste será: S.F(N) - S.F(N-2).
E assim até um mês antes do reajuste, quando a última perda corrigida será: S.F(N) - S.F(1).
A soma das perdas corrigidas é composta da soma de um termo constante S.F(N) e de uma progressão geométrica, cuja expressão é:
Para expressar a soma das perdas relativa ao salário reajustado S.F(N) dividimo-la por este termo resultando:
Como exemplo, tomemos um caso com reajustes anuais (N=12) e uma inflação mensal média de i = 1%. Então:
ou seja, se o salário atualizado na época do reajuste for de (digamos) $ 1.000, a perda havida nos 12 meses terá sido de $ 632.
Observação:
Notemos que não foi considerada a existência do 13º salário na dedução da fórmula. Assim, perdas de 100% (1 salário) para N = 12 meses, ou de 50% (0,5 salário) para N = 6 meses, ficam de certo modo compensadas com o 13º salário.