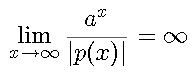P versus NP

Pedro Luiz Aparecido Malagutti
http://www.dm.ufscar.br/hp/hp501/hp501001/hp501001.html

A Complexidade Computacional é um ramo da Matemática Computacional que estuda a eficiência dos algoritmos. Do ponto de vista prático, de nada nos adianta um algoritmo perfeito se sua implementação computacional demora uma centena de anos para ser processada. Mesmo tarefas relativamente simples, como o produto de dois números com muitos dígitos, pode demorar alguns minutos para serem concluídas nos atuais computadores. Se considerarmos que alguns algoritmos necessitam multiplicar números muito grandes milhares de vezes esses alguns minutos podem se transformar em um tempo excessivamente longo.

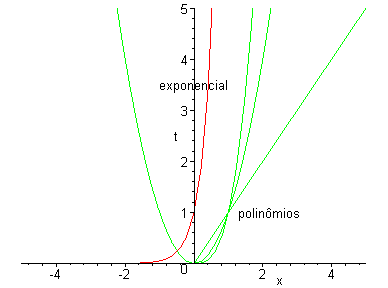
Para medir a eficiência de um algoritmo freqüentemente usamos o tempo teórico que o programa leva para encontrar uma resposta em função dos dados de entrada. Este cálculo é feito associando-se uma unidade de tempo para cada operação básica que o procedimento executa. Se a dependência do tempo com relação aos dados de entrada for polinomial, o programa é considerado rápido. Se, entretanto, a dependência do tempo for exponencial o programa é considerado lento. Podemos também nos perguntar sobre os programas que estão entre estas duas classes.

Dado um polinômio p(x) sabemos que |p(x)| cresce para infinito com |x|. Esse crescimento, entretanto, é lento quando comparado com o crescimento de uma função exponencial ax, onde a 1. Este fato pode ser expresso pela fórmula

Definição: A classe de algoritmos P é formada pelos procedimentos para os quais existe um polinômio p(n) que limita o número de passos do processamento se este for iniciado com uma entrada de tamanho n.

Os algoritmos NP não se referem a procedimentos não polinomiais (na verdade isto é uma conjectura). A leitura correta para procedimentos NP é dizer que se referem a algoritmos "não-determinísticos polinomiais" no tempo. A classe NP será definida logo abaixo; antes vamos fazer uma breve abordagem histórica de suas origens.

No início dos anos sessenta foram encontrados muitos algoritmos que resistiam a uma simplificação polinomial, isto é, algoritmos que não admitiam procedimentos análogos na classe P. Nesta época Steve Cook [1] observou um fato simples e ao mesmo tempo surpreendente: se um problema pudesse ser resolvido em tempo polinomial, poderíamos também verificar se uma dada possível solução é correta em tempo polinomial (dizemos que o algoritmo pode ser certificado em tempo polinomial).

Um exemplo simples de como esta certificação pode ser feita é o problema de descobrir se um dado número é composto, ou seja, se ele não é primo. Suponha que queiramos descobrir se 4294967297 é um número composto. Não existe uma maneira eficiente (rápida) de fazer isto. De fato tal tarefa pode ser realizada pela utilização do crivo de Eratóstenes, testando os possíveis divisores do número, o que pode demandar um tempo excessivo de computação. Entretanto existe uma maneira sucinta de certificar que aquele número é composto: basta verificar que o produto de 6700417 por 641 é exatamente 4294967297. Assim, se pudermos achar uma certificação, podemos exibir efetivamente sua validade. Achá-la pode ser extremamente difícil, no entanto. A fatoração de 4294967297 foi encontrada por Leonard Euler em 1732, noventa e dois anos após Pierre de Fermat ter conjecturado erroneamente que tal número era primo.

Definição: A classe dos problemas NP é aquela para as quais podemos verificar, em tempo polinomial, se uma possível solução é correta.

Evidentemente P NP. De fato, se um algoritmo pode ser executado em tempo polinomial e tivermos em mãos um possível candidato S à solução, é possível executar o programa, obter uma solução correta C e comparar C com S para certificar que S é de fato solução, tudo em tempo polinomial.

O problema P versus NP consiste na seguinte conjectura:

A classe NP consiste dos algoritmos não-determinísticos polinomiais, e recebe este nome devido a uma formulação equivalente que não usa o conceito de certificação, mas o de decisão de linguagens. Infelizmente a demonstração desta equivalência é bastante técnica; ela pode ser encontrada em [5]. A categoria de linguagens a que nos referimos são as reconhecidas por computadores teóricos chamados de Máquinas de Turing. Tais máquinas parecem capturar completamente o sentido do termo computação.

Uma máquina de Turing pode ser pensada como uma fita infinita de papel, dividida em pequenas casas, e um lápis/borracha especial que pode seguir instruções. Essas instruções são bastante simples: o lápis pode ler um símbolo na fita e, analisando-o, pode apagá-lo e escrever por cima do símbolo lido e, mudando de estado, pode se mover para a direita ou para a esquerda para analisar um novo símbolo, ou simplesmente parar.

Existe uma afirmação heurística, conhecida como Tese de Church, que diz que tudo o que pode ser programado algoritmicamente pode também ser realizado por uma máquina de Turing. Um simulador muito interessante de uma máquina de Turing pode ser encontrado no endereço: http://www.cheran.ro/vturing/download.html.

Alan Mathison Turing foi um brilhante matemático inglês, tendo trabalhado em várias áreas, como Lógica, Álgebra, Teoria dos Números, Computação, Inteligência Artificial, Morfogênese. Dedicou-se durante algum tempo à arquitetura de computadores. Em Lógica deu continuidade ao Teorema da Indecidibilidade de Kurt Gödel, demonstrando que não existe um algoritmo universal capaz de detectar proposições indecidíveis em um sistema axiomático. Para isso usou um dispositivo muito simples, hoje chamado Máquina de Turing. Durante a 2a Guerra Mundial trabalhou para o governo britânico como decifrador de códigos, tendo desempenhado importante papel na criptoanálise do código alemão conhecido com "Enigma".

Alan M. Turing 1912-1954

Existem máquinas de Turing determinísticas e não-determinísticas. As determinísticas são aquelas que quando estão em um certo estado, lendo um certo dado, podem se movimentar de um único modo rumo à próxima configuração; já as não-determinísticas podem se mover para diversas configurações, a partir do dado lido e da configuração interna atual. Evidentemente as máquinas determinísticas formam uma subclasse das não-determinísticas.

Que ligação afinal existe entre máquinas de Turing e linguagens? Em termos breves, se L é uma linguagem sobre um alfabeto S, isto é, se L é um subconjunto finito de seqüências de letras de S, dizemos que uma máquina de Turing M aceita a linguagem L se para toda palavra construída com as letras de S colocada como entrada (input), após o processamento M entra em um estado de aceitação (respondendo de algum modo sim) se a palavra pertencer à linguagem. A palavra é recusada por M se, após o processamento M entra num estado de rejeição (respondendo não de algum modo) ou se ela falhar em completar seu processo computacional.

Neste contexto, o problema P versus NP assume a seguinte forma:

Quais conseqüências a resolução positiva desta conjectura pode trazer? Destacamos apenas três:

• a existência de algoritmos úteis para uma série de problemas computacionais práticos nas indústrias;

• a destruição da segurança nas transações financeiras feitas eletronicamente;

• a quebra no sigilo de trocas de informações diplomáticas, Internet, etc.

A possível destruição dos códigos de segurança se deve ao fato de que a maioria dos algoritmos criptográficos são construídos sobre a hipótese da impossibilidade de uma criptoanálise em tempo polinomial (ver [3]).

Finalmente gostaríamos de destacar uma importante subclasse dos problemas NP, que são os problemas NP-completos. Leonid Levin [2] e Steve Cook [1] observaram que, dentre os problemas NP, existem alguns que são mais difíceis do que outros, no sentido de que, se pudermos resolver um desses problemas em tempo polinomial, então todos os problemas em NP também podem ser resolvidos em tempo polinomial. Assim a classe dos problemas NP-completos é o subconjunto dos "mais difíceis" problemas não-determinísticos polinomiais. Atualmente são conhecidos uma quantidade enorme de problemas NP-completos, mas o mais famoso deles talvez seja o Problema do Caixeiro Viajante, também designado por TSP (Traveling Salesman Problem):

A solução deste problema, por ser ele NP-completo, pode levar à destruição de quase todos os sistemas de segurança eletrônicos do mundo!

Para obter mais informaçõs na Internet:

[1] Para mais detalhes veja sobre o problema TSP consulte http://www.ing.unlp.edu.ar/cetad/mos/TSPBIB_home.html.

[2] Para ver as biografias dos matemáticos que são citados nesta página consulte
MacTutor History of Mathematics.

[3] Para informações adicionais sobre Alan M. Turing consulte
The Alan Turing Home Page.

Referências.

[1] Cook, S., The complexity of theorem-proving procedures. New York, Proceedings of the 3^rd Symposium on the Theory of Computing, ACM, 151-158.

[2] Levin, L., Universal Search Problems, Probl. Pered. Inf. 9(3), 1973. Veja também Annals of the History of Computing, 6(4): 384-400, 1984.

[3] Adleman, L., Rivest, R. e Shamir, A method for obtaining digital signature and public-Key cryptosystems. Comm. ACM, 21(2), 1978.

[4] Smale, S., Mathematical Problems for the next century. MATHINT: The Mathematical Intelligencer, 20, 1998.

[5] Lewis B. and Papadimitriou C., Elements of Theory of Computation. Prentice Hall, 1981.

[6] Costa, N., Máquina corre atráz do cérebro. Folha de São Paulo, 28 de novembro de 1993.

Artigo apresentado para publicação em janeiro de 2001 por Pedro Luiz Aparecido Malagutti, professor do DM-UFSCar. As figuras foram construídas pelo autor. A foto de Turing foi adaptada de The Alan Turing Home Page. Texto preparado para publicação na Internet por Roberto R. Paterlini, do DM-UFSCar.

Publicado em 01/2001. Atualizado em 12-mai-2002.